Aim
In this post we are going explore the possibilities of collating the input parameters and results of function to make summary tables or plots. We are aiming to write a small utility that does this task for us.
Motivation
Frequently, we pass parameters as keywords to a function, hence we restrict or attention to keyword arguments for the rest of the discussion. For example, the number iterations n_iter and the number of independent runs max_init are specified as keywords for the multidimensional scaling algorithm of scikit-learn (sklearn.manifold.MDS).
We start with a collection of parameters over which the function will be run. It appears that scikit-learn lacks a strightforward way to collate the keyword aruments and the results. One can invoke the cross validating utility, GrigSearchCV of scikit-learn, however we are are not interested in validating our result at this stage. Our aim is to obtain a rough boundaries of the sensible parameter space or just generate a grid of results.
The aforementioned module does contain an extremely useful functionality ParameterGrid. This returns an iterator over keyword–value pairs created from the dictionary.
from sklearn.model_selection import ParameterGrid
param_dict = {'param1' : ['a', 'b', 'c'],
'param2' : [1, 2] }
param_grid = ParameterGrid(param_dict)
for params in param_grid:
print(params)
{'param1': 'a', 'param2': 1}
{'param1': 'a', 'param2': 2}
{'param1': 'b', 'param2': 1}
{'param1': 'b', 'param2': 2}
{'param1': 'c', 'param2': 1}
{'param1': 'c', 'param2': 2}
We are trying to find ways to collate the results of a function whith its input parameters into a structure similar to the one below, where the third column represents the output from the function:
{'param1': 'a', 'param2': 1, 'result' : res1}
{'param1': 'a', 'param2': 2, 'result' : res2}
{'param1': 'b', 'param2': 1, 'result' : res3}
{'param1': 'b', 'param2': 2, 'result' : res4}
{'param1': 'c', 'param2': 1, 'result' : res5}
{'param1': 'c', 'param2': 2, 'result' : res6}
Preliminaries
Firstly, we create a toy function called calculate_distance that calculates the $L_{p}$ distance between two real vectors. This function takes a small number of keyword arguments.
- dist_type can be ‘eucledian’ or ‘lp’
- power is the order of the norm. It is ignored when dist_type is ‘eucledian’
- scale is factor to scale the distance with
#---------------------------
def _lp_distance(x1, x2, power = 1, scale = 1.0):
#---------------------------
"""
Caclulates the distance between two 1D vectors in Lp sense.
Parameters:
x1, x2 (np.ndarray[n_size]) : two vectors of shape (n_size,)
power (int or float) : power of norm. Default power = 2.
scale (float) : factor to scale the distance with. Default scale = 2.
Returns:
distance (np.float) : the scaled distance between x1 and x2
"""
# --- check input
if x1.size != x2.size:
raise ValueError("Unequal length vectors")
if (x1.ndim != 1) or (x2.ndim != 1):
raise ValueError("Only 1D vectors are accepted")
if power < 1:
raise ValueError("Keyword 'power' must be 1 <. Got: {0}".format(power))
# --- calculate Lp norm
distance = np.power(np.sum(np.power(np.abs(x1 - x2), power)), 1.0 / power)
# --- scale distance
distance *= scale
return distance
#---------------------------
def _eucledian_distance(x1, x2, scale = 1.0):
#---------------------------
"""
Calculates the Eucledian distance between two vectors
x1, x2 (np.ndarray[n_size]) : two vectors of shape (n_size,)
scale (float) : factor to scale the distance with. Default scale = 2.
Returns:
distance (np.float) : the scaled Eucledian distance between x1 and x2
"""
return _lp_distance(x1, x2, power = 2, scale = scale)
#---------------------------
def calculate_distance(x1, x2, dist_type = "eucledian", power = 2, scale = 1.0):
#---------------------------
"""
Calculates the distance between two 1D vectors
Parameters:
x1, x2 (np.ndarray[n_size]) : two vectors of shape (n_size,)
dist_type (str) : 'eucledian', lp, default = 'eucledian'
power (int or float) : power of norm. Default power = 2.
scale (float) : factor to scale the distance with. Default scale = 2.
Returns:
distance (np.float) : the scaled distance between x1 and x2
"""
if dist_type == "eucledian":
distance = _eucledian_distance(x1, x2, scale = scale)
elif dist_type == "lp":
distance = _lp_distance(x1, x2, power = power, scale = scale)
else:
raise ValueError("dist_type: must be {0} or {1}. Got: {2}.".format("eucledian", "lp", dist_type))
return distance
It is now all set to write our own utilities to group the keywords and the return values. After initialising the trial vectors:
# set up
import numpy as np
n_size = 10
x1 = np.random.rand(n_size)
x2 = np.random.rand(n_size)
1. solution: numpy structured arrays (slow and dirty)
We are going to store the parameter values and the result in a structured numpy array. The field names are the keyword names and the res token for the result.
Algorithm
- Create an empty list
result_gridto store the parameters and results - Loop over the parameters
- Evaluate function
- Append result to
result_grid - Create a tuple with the parameter and result values
- Append tuple to storage
- Create a
np.dtypecalledresult_grid_typefor the parameters - Append the name and the type of the result to
result_grid_type - Cast
result_gridto a numpy structured array of typeresult_grid_type
# create grid of parameters.
param_dict = {'power' : [1, 2, 10],
'scale' : [1.0, 2.0]}
param_grid = ParameterGrid(param_dict)
result_grid = []
for params in param_grid:
res = calculate_distance(x1, x2, **params)
# collate parameters and corresponding result
result_grid.append((*params.values(), res))
# create a datatype 1. type of parameters
result_grid_type = [(_k, type(_v)) for _k, _v in params.items()]
# append type of result -- we assume it does not change during the iteration.
result_grid_type.append(('res', type(res)))
result_grid = np.array(result_grid, dtype = np.dtype(result_grid_type))
The lines
result_grid_type = [(_k, type(_v)) for _k, _v in params.items()]
result_grid_type.append(('res', type(res)))
np.dtype(result_grid_type)
construct a numpy dtype instance, a list of tuples. The first element in each tuple is the field name, the second one is the type of the contained data.
print(np.dtype(result_grid_type))
[('power', '<i4'), ('scale', '<f8'), ('res', '<f8')]
The records are conveniently accessed by their names:
print("power : ", result_grid['power'])
power : [ 1 1 2 2 10 10]
print("res : ", result_grid['res'])
res : [1.24999113 2.49998226 1.24999113 2.49998226 1.24999113 2.49998226]
Note,it seems to work for at least float and integer parameters. However, we run into problems immediately once we try to use keywords that have variable length string values. Consider summarising the problem and then linking to more details.
A quick fix is to introduce the _set_ptype function which finds the longest string in a list and sets the type accordingly. The type calls should be changed according to
type(x) --> _set_ptype(type(x)) to avoid clipping of strings.
def _set_ptype(pvals):
"""
Utility to generate numpy compatible string formats.
If the parameters are a list of string it
chooses the longest of them as the length in the type descript
Parameters:
pvals ([]) : list of parameters
Returns:
p_type (type subclass or string) : parameter type
"""
p_type = type(pvals[0]) # shortcut at first element
if p_type is not str:
return p_type
max_string_len = max(list(map(lambda x : len(x), pvals)))
p_type = 'U'+str(max_string_len)
return p_type
2. solution: defaultdict and pandas dataframe (quick and dirty)
A considerably more convenient solution is to use defaultdicts and a Pandas dataframe to collate the results. Pandas will take care of setting the types. The result_dict is a defaultdict whose default values are lists. The keys are the keywords for the parameters and the res token for the results.
Algorithm
- Initialise an empty dictionary of lists
result_dictto store parameters and results - Loop over parameters
- Evaluate function
- Append the parameter values to the correspnding lists
- Append the result value to the
reslist
- Convert
result_dictto pandas dataframe
from collections import defaultdict
import pandas as pd
result_dict = defaultdict(list)
for params in param_grid:
res = calculate_distance(x1, x2, **params)
[result_dict[_k].append(_v) for _k, _v in params.items()]
result_dict['res'].append(res)
result_df = pd.DataFrame.from_dict(result_dict)
result_df
| power | res | scale | |
|---|---|---|---|
| 0 | 1 | 1.249991 | 1.0 |
| 1 | 1 | 2.499982 | 2.0 |
| 2 | 2 | 1.249991 | 1.0 |
| 3 | 2 | 2.499982 | 2.0 |
| 4 | 10 | 1.249991 | 1.0 |
| 5 | 10 | 2.499982 | 2.0 |
3. solution: dictionary and pandas (quick, with better hygiene standards)
There might be some cases when some of the keywords become meaningless e.g. passing power = n when calculating the Eucledian norm with the dist_type = 'euclidian' option. In order to avoid surplus runs, ParameterGrid allows us to create a list of dictionaries.
param_dict = [{'dist_type' : ['eucledian'],
'scale' : [1.0, 2.0]},
{'dist_type' : ['lp'],
'power' : [1, 3],
'scale' : [1.0, 2.0]}]
param_grid = ParameterGrid(param_dict)
for params in param_grid:
print(params)
{'dist_type': 'eucledian', 'scale': 1.0}
{'dist_type': 'eucledian', 'scale': 2.0}
{'dist_type': 'lp', 'power': 1, 'scale': 1.0}
{'dist_type': 'lp', 'power': 1, 'scale': 2.0}
{'dist_type': 'lp', 'power': 3, 'scale': 1.0}
{'dist_type': 'lp', 'power': 3, 'scale': 2.0}
As a consequence, we are going to collect the parameters and the result in a list of dictionaries and convert that to a pandas dataframe.
Algorithm
- Create empty list for storage
result_list - Loop over parameters
- Evaluate function
- Create a dictionary,
_res_dictof parameters - Update dictionary with the result
- Append to storage,
result_list
- Convert
result_listtopandas dataframe
result_list = [] # storage for parameters and results for all runs
for params in param_grid:
res = calculate_distance(x1, x2, **params)
_res_dict = dict(**params) # store parameters. Do not contaminate params dict
_res_dict.update({'res' : res}) # append result to dictionary
result_list.append(_res_dict)
result_df = pd.DataFrame(result_list)
result_df
| dist_type | power | res | scale | |
|---|---|---|---|---|
| 0 | eucledian | NaN | 1.249991 | 1.0 |
| 1 | eucledian | NaN | 2.499982 | 2.0 |
| 2 | lp | 1.0 | 3.035391 | 1.0 |
| 3 | lp | 1.0 | 6.070782 | 2.0 |
| 4 | lp | 3.0 | 0.982607 | 1.0 |
| 5 | lp | 3.0 | 1.965213 | 2.0 |
We can see that the power parameter is replaced with NaN-s, where it is not used. They can easily be tidied up with calling
result_df['power'].fillna(0, inplace = True)
The apt reader have surely recognsised that Solutions 1. and 2. were subclasses of the one discussed here.
4. solution: get_params(), dictionary and pandas dataframe (quick, remarkable personal hygiene)
The scikit-learn estimators, classifiers etc. usually have a built in get_params() method that retrieves all of the parameters. This can be used in conjuction with the method above. In the following example we try to estimate down the minimum required number of runs and iterations to minimse stress in multidimensional scaling. (N.B. obviously, one might wish to cross-validate these results.)
Algorithm
- Create empty list for storage
result_list - Loop over parameters
- Evaluate function
- Create a dictionary,
_res_dictof parameters - Retrieve the estimator’s parameters with
get_params() - Update dictionary with the result
- Append to storage,
result_list
- Convert
result_listtopandas dataframe
from sklearn.manifold import MDS
# generate a 10D random data set
n_samples, n_features = 100, 10
X = np.random.rand(n_samples, n_features)
# number of SMACOF cycles and restarts
param_dict = { 'max_iter' : [10, 100, 300, 500],
'n_init' : [1, 2, 5, 10]}
param_grid = ParameterGrid(param_dict)
# instantiate transformer
mds = MDS()
# explore parameter space
result_list = []
for params in param_grid:
mds.set_params(**params)
mds.fit_transform(X)
_res_dict = mds.get_params()
_res_dict.update({'stress' : mds.stress_})
result_list.append(_res_dict)
result_df = pd.DataFrame(result_list)
The resultant dataframe looks like:
result_df.head()
| dissimilarity | eps | max_iter | metric | n_components | n_init | n_jobs | random_state | stress | verbose | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | euclidean | 0.001 | 10 | True | 2 | 1 | 1 | None | 1411.660030 | 0 |
| 1 | euclidean | 0.001 | 10 | True | 2 | 2 | 1 | None | 1376.313335 | 0 |
| 2 | euclidean | 0.001 | 10 | True | 2 | 5 | 1 | None | 1337.258374 | 0 |
| 3 | euclidean | 0.001 | 10 | True | 2 | 10 | 1 | None | 1315.719648 | 0 |
| 4 | euclidean | 0.001 | 100 | True | 2 | 1 | 1 | None | 1017.204895 | 0 |
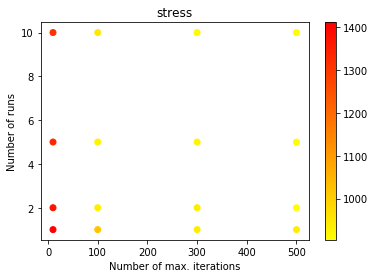
We can now visually inspect which are the optimal parameters.
from matplotlib import pyplot as plt
cmap = plt.get_cmap('hot_r')
plt.title('stress')
plt.xlabel('Number of max. iterations')
plt.ylabel('Number of runs')
plt.scatter(result_df['max_iter'], result_df['n_init'],
cmap = plt.get_cmap('autumn_r'), c = result_df['stress'])
plt.colorbar()
plt.show()
Summary
In this post we have designed a couple of generic frameworks to collate keyword parameters of a function and its result. They based on grouping the parameters and results in an intermediary data objects, such as list of dictionaries, then injecting these groups to a single keyable data structure.