Comparing large arrays

Aim

In this post we are going write a utility that compares large arrays efficiently which can then be used to label clusters. First of all, it should be defines what is meant by large and efficiently. Large refers to arrays that are longer than 1000. A efficient algorithm scales better than $O(N^2)$ where $N$ is the number of arrays.

Motivation

I am currently working on implementing a clustering algorithm, Markov cluster algorithm, where each cluster has an associated row vector in the transtion matrix:

Rows 1. and 5. denotes the same cluster which consists of the first three nodes, whereas the second and seventh row belong to two different clusters. By finding the unique rows one can assign the cluster labels to the nodes.

Initial considerations

Speed

Unfortunately, python is not designed for numerical heavy programming tasks, therefore a native python implementation where we perform $N^{2}$ array comparisons would definitely be a suboptimal solution. In general, most of the time one is primarily concered with overcoming the speed limitations of python when implementing numerical algorithms. The usual pathways are

1. Write the numerically demanding parts in a compiled language (e.g. C, fortran)
2. Write the code in cython which is then compiled
3. Use compiled python libraries (e.g. numpy)
4. Write the code in python and use a just in time compiler (e.g. numba)
5. Rephrase the problem so that it becomes tractable in native python

Data format – sprase matrices

The matrices are stored in the compressed sparse row (csr) format.

A csr matrix consists of three arrays. One that stores the nonzero (nnz) elements of the matrix, one that stores the column indices and a third one that stores the accumulative number of nnz entries for each row. These are called sparse_matrix.data, sparse_matrix.inidces, sparse_matrix.indptr in the scipy.sparse parlance.

Our hypothetical matrix from the first paragraph would look like

sparse_matrix.data = [a, a, a, b, b, a, a, a,..., c, c]
sparse_matrix.indices = [0, 1, 2, 3, 4, 0, 1, 2,..., N-2, N-1]
sparse_matrix.indptr = [0, 3, 5, 5, 5, 8, 8,..., 8, 10]

Meaningful data

One can readily observe that only the column indices carry information on the clusters. The actual values are redundant for they are equal for a given column index. As a consequence, one only has to compare the column indices of the rows. The first task is then to retrieve the column indices for each row.

Possible solutions

1. solution: breaking down to smaller groups.

Two rows are definitely different if the number of their nnz entries are not equal. Therefore if we group the rows according to their length (length from now on refer to the number of nnz elements), the comparison should only be carried out in the so-created groups. The cost still would be $(N/k)^{2} \approx O(N^{2})$. It is not great, but can serve as a starting point.

Algorithm

We are going to use defaultdict to store the vectors of equal length; and three generators, islice, map and filter to speed up the iteration over the column indices.

from collections import defaultdict
from itertools import islice

def group_rows_by_length(a):
    """
    Groups the rows or columns of a csr or csc sparse matrix according to their length.
    Parameters:
        a ({scipy.sparse.csr_matrix, scipy.sparse.csc_matrix) : matrix
    Returns:
        storage ({int : [[]]}) : dictionary where the keys are the length of the rows, the values the list of rows.
    """
    storage = defaultdict(list)
    nnz_in_rows = np.diff(a.indptr)
    [storage[len(x)].append(x) for x in map(lambda y: list(islice(a.indices, y)), filter(lambda z: z > 0, nnz_in_rows))]
    
    return storage

All scipy sparse matrices implement the tolil() method which recasts the matrix to a list of lists format. In fact, we tacitly did exactly the same above. The tolil() source code can be found here. The only drawback of using tolil() that it copies the data across to the new lil matrix instance – a costly step.

2. solution #hash

What aspects of the previous solution can be improved?

1. We will still have to compare the vectors. Albeit, only smaller groups of them.
2. We are still using a native python loop in the form of loop comprehension.
3. Updating the dictionary is expensive.

As to the last issue, do we really need to store the indices? Can we use the indices themselves as keys instead? If so, the keys of the dictionary can solely used to identify the various vectors. Yes we can! Only modification that we have to do is to cast the nozero indices as tuple-s as opposed to list-s, so that they can be hashed.

Algorithm

In python:

import numpy as np

def select_unique_rows(a):
    """
    Selects the unique rows from a csr/csc matrix.
    Parameters:
        a ({scipy.sparse.csr_matrix,scipy_sparse.csc_matrix}) a sparse matrix.
    Returns:
        unique_rows ({:}) : the keys of the dictionary are tuples of the column indices of the unique rows.
        The values are the last occurences of the unique rows.
    """
    nnz_in_rows = np.diff(a.indptr)
    unique_rows = {tuple(islice(a.indices, int(x))) : y for y, x in enumerate(filter(lambda x: x > 0, nnz_in_rows))}
    
    return unique_rows

If we do not care about the row indices (and we do not really), the enumerate() constructor can be removed:

def select_unique_rows_lite(a):
    """
    Selects the unique rows from a csr/csc matrix.
    Parameters:
        a ({scipy.sparse.csr_matrix,scipy_sparse.csc_matrix}) a sparse matrix.
    Returns:
        unique_rows ({:}) : the keys of the dictionary are tuples of the column indices of the unique rows.
        The values are set to unit
    """
    nnz_in_rows = np.diff(a.indptr)
    unique_rows = {tuple(islice(a.indices, int(x))) : 1 for x in filter(lambda x: x > 0, nnz_in_rows)}
    
    return unique_rows

Furthermore, we can only keep the keys, for the values carry no useful information. This can be achieved by using set as opposed to tuple:

def select_unique_rows_lite_wset(a):
    """
    Selects the unique rows from a csr/csc matrix.
    Parameters:
        a ({scipy.sparse.csr_matrix,scipy_sparse.csc_matrix}) a sparse matrix.
    Returns:
        unique_rows ({}) : set of tuples of column indices of the unique rows.
    """
    nnz_in_rows = np.diff(a.indptr)
    unique_rows = set(tuple(islice(a.indices, int(x))) for x in filter(lambda x: x > 0, nnz_in_rows))
    
    return unique_rows

Much better. There are a number issues, though.

1. Filtering can be expensive. It will always be a tradeoff between how many nnz rows we have, and much time filtering takes. Usually, we will not have any if we treat the csr matrix properly.
2. We still iterating in native python.

def select_unique_rows_lite_nofilter(a):
    """
    Selects the unique rows from a csr/csc matrix.
    Parameters:
        a ({scipy.sparse.csr_matrix,scipy_sparse.csc_matrix}) a sparse matrix.
    Returns:
        unique_rows ({:}) : the keys of the dictionary are tuples of the column indices of the unique rows.
        The values are set to unit
    """
    nnz_in_rows = np.diff(a.indptr)
    unique_rows = {tuple(islice(a.indices, int(x))) : 1 for x in nnz_in_rows}
    
    return unique_rows

Once the clusters are determined, one can create an array of the cluster labels. assign_cluster_labels does this job for the select_unique_rows_lite, select_unique_rows_lite_wset and select_unique_rows_lite_nofilter functions. Again, filtering can be removed if we made sure there are no empty rows in the matrix.

def assign_cluster_label(clusters):
    n_nodes = sum(map(lambda x: len(x), clusters))
    
    labels = np.full(n_nodes, -1, dtype = np.int)
    for label, cluster in enumerate(filter(lambda x: len(x) > 0, clusters)):
        labels[np.array(cluster)] = label

3. Solution: Colouring

Imagine the nodes as an array of beads of uniform colour. We than paint the beads belonging to the same cluster with the same colour. Once all of the beads are painted they have all been assigned to a cluster. We are going to implement this solution using numba.

import numba
@numba.jit(nopython=True)
def colour_array_numba(idcs, iptr, labels):
    """
    Assigns labels.
    Parameters:
      idcs (np.ndarray of np.int) : csr indices
      iptr (np.ndarray of np.int) : csr row pointers
      labels (np.ndarray of np.int) : initialised label array
    """

    n_nodes = iptr.size - 1  # number of nodes
    i_label = 0              # "colour" 
    n_coloured = 0           # number of coloured nodes

# --- loop over all rows <--> vectors <--> clusters
    for i in range(n_nodes):
# grep a cluster
        i_start, i_end = iptr[i],  iptr[i+1]
        n_nodes_in_cluster = i_start - i_end
# skip if it is empty
        if n_nodes_in_cluster == 0: continue

        inodes = idcs[i_start:i_end]
# if already coloured skip
        if labels[inodes[0]] != -1: 
          continue
        else:
# assign colour
          labels[inodes] = i_label
          i_label += 1
# keep track of coloured nodes
          n_coloured += n_nodes_in_cluster
# shortcut if all nodes have been coloured
          if n_coloured == n_nodes:
            break

def assign_labels(a):
  """
  Assigns a label to the nodes 
  Parameters:
    a (scipy.sparse.csr_matrix) : sparse matrix
  Returns:
    labels (np.ndarray of np.int) : cluster label for each node
  """
# --- create an array of uniform labels
  labels = np.full(a.shape[1], -1, dtype = np.int)
# --- colour nodes according to clusters
  colour_array_numba(a.indices, a.indptr, labels)

  return labels

Testing

We are going to compare the above methods on the sets created with our efficient create_block_diagonal_csr_matrix_np utility.

import sys
sys.path.append(r'C:\Users\Balazs\source\repos\MPC\MPC\RandomSparse')
from BlockDiag import create_block_diagonal_csr_matrix_np

In the following paragraph, we create a number of cluster groups in the csr representation. The size and nuber of clusters vary between 10 and 1000. Only 5% of the row vectors is retained in each block. In the largest example, it means 1000 times 50 vectors of length of 1000 nodes each.

from sklearn.model_selection import ParameterGrid

parameter_grid = ParameterGrid({'cluster_size' : [10, 50, 100, 200, 500, 1000],
                                'n_clusters' : [10, 50, 200, 500, 1000]})

keep_density = 0.05
keep_each_row = True

As to timing, I wrote a bare bones timer utility, SlimTimer, which will be invoked to measure the execution times.

sys.path.append(r'c:\users\Balazs\source\repos\slimTimer')
from slimTimer.SlimTimer import SlimTimer 

# set up a timer for each function with nine runs to measure each
n_runs = 5

timers = [SlimTimer(func = select_unique_rows_lite, n_runs = n_runs),
          SlimTimer(func = select_unique_rows_lite_wset, n_runs = n_runs),
          SlimTimer(func = select_unique_rows_lite_nofilter, n_runs = n_runs),
          SlimTimer(func = assign_labels, n_runs = n_runs)]

We will now measure how the functions perform for each matrix sequentially.

timings = []
for params in parameter_grid:
    
# create blocks i.e. groups of clusters
    clusters = [params['cluster_size']] * params['n_clusters']
    
# set up matrix    
    mat = create_block_diagonal_csr_matrix_np(clusters, fill_value = 1, 
                                              keep_density = keep_density, 
                                              keep_each_block = True)
# measure labeling time
    for timer in timers:
        timer.set_func_args(mat)
        timer.measure()

# get timing results
    res_dict = params.copy()
    for timer in timers:
        res_dict.update(timer.to_dict(with_tag = True))

# collect results
    timings.append(res_dict)

We will plot the comparisions grouped by the the size of the clusters.

import pandas as pd
import matplotlib.pyplot as plt

df = pd.DataFrame(timings)
grouped = df.groupby('cluster_size')

In case you wish to use this notebook, the header of the dataframe shown below. We will need the n_cluster , function_name_tmean and function_name_tstdev columns to plot the timings, which contain the number of clusters, the mean runtime and the standard error of the mean time for each labeling function.

print(df.columns)

Index(['assign_labels_runtimes', 'assign_labels_tmean', 'assign_labels_tstdev',
       'cluster_size', 'n_clusters',
       'select_unique_rows_lite_nofilter_runtimes',
       'select_unique_rows_lite_nofilter_tmean',
       'select_unique_rows_lite_nofilter_tstdev',
       'select_unique_rows_lite_runtimes', 'select_unique_rows_lite_tmean',
       'select_unique_rows_lite_tstdev',
       'select_unique_rows_lite_wset_runtimes',
       'select_unique_rows_lite_wset_tmean',
       'select_unique_rows_lite_wset_tstdev'],
      dtype='object')

The comparison of the timing of the various functions can be seen below.

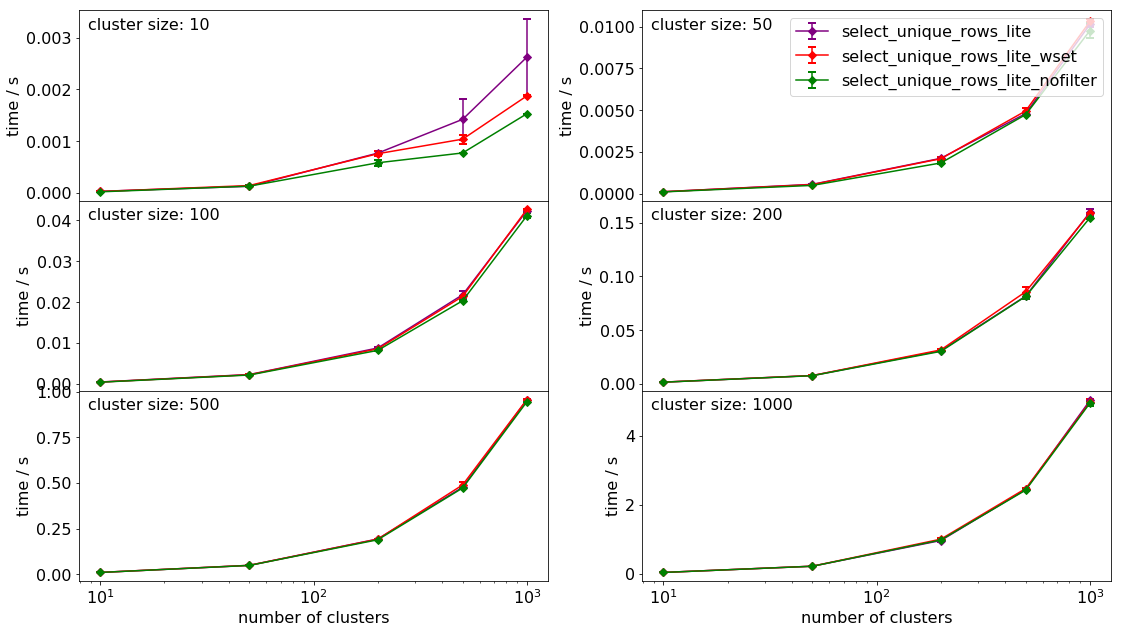
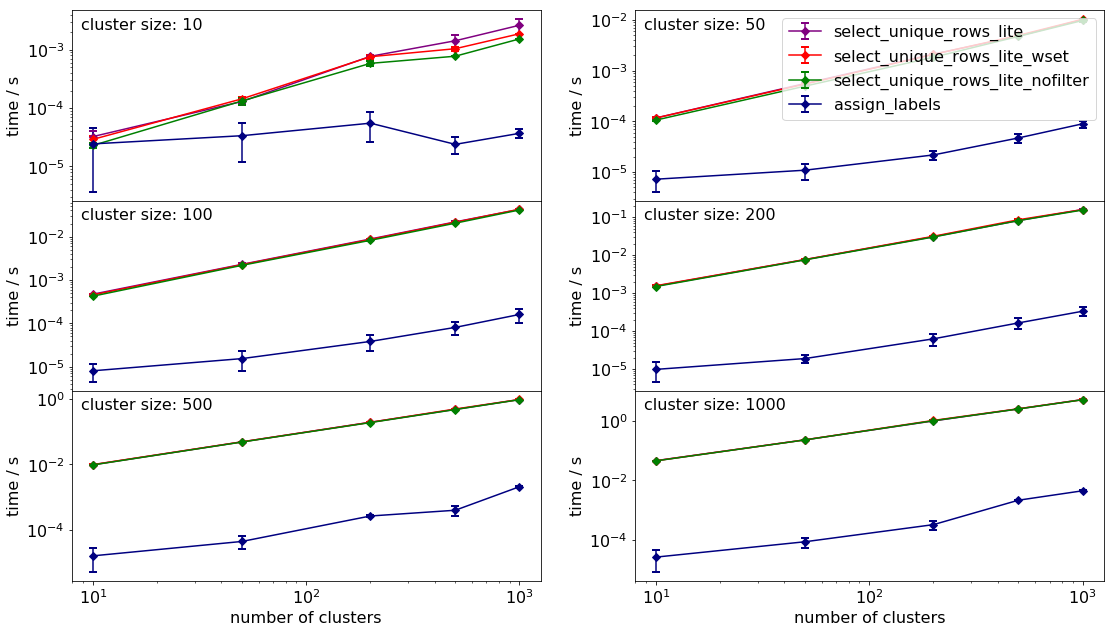
It is of no surprise that the compiled function is the fastest for all sizes and numbers of clusters by a long chalk. As to the native python methods, ommission of filtering speeds up the process. One can also observer that costructing sets is slower than constructing a dictionary for our purposes.

Conclusions

We wrote and compared native python and compiled utilities to label clusters. We have found that the compiled utility is superior to the native python ones. Whether to use it? I would argue that if efficiency is the most important desideratum of our program, one should never by shy to use the tools to achive it.