This post is the second part of the discussion of classifying climates. In the previous one we explored the structure of the data and optimised a k nearest neighbour classifier. The objectives this time are
- build a data pipeline
- use neural networks to classify the climate data
The raw notebook can be found here.
The Data
The data comprises of 24 numerical records and a label. The first twelve dimensions of the numerals are the monthly mean temperature in celsius degrees times ten. The second half lists the monthly mean precipitation in milimetres.
Data flow
Much like in a real world, scenario we do not posses the entire dataset in advance. Each step in the data pipeline therefore has to be reuseable. In the previous post the data was preprocessed before the feature engineering step. This time, the preprocessing steps are incorporated in the pipeline.
Preprocessing
Transformation
The temperature and precipitation data are in different ranges and heavily riddled with outliers. We therefore use Yeo–Johnson transforms separately on the two sets.
Power transform on flattened arrays
All features in a set should undergo identical transformation to preserve the relative positions of the data e.g. July’s temperatures should be transformed exactly in the same way as December’s temperatures are. For the transformer classes operate along each dimension, we write a wrapper which takes a 2D array and flattens it to 1D before the fitting and transformation. It restores the original shape of the transformed array afterwards. The wrapper is implemented in the create_flat_transformer function below. It takes a transformer class and decorates its fit, transform and fit_transform methods.
def create_flat_transformer(transformer):
"""
Wrapper to perform the transformation on the flattened input array to 1D
The X argument is transformmed:
(n_samples, n_features) --> (n_samples * n_features, 1)
It preserves the methods and attributes of the underlying estimator.
Parameters:
transformer (object) : should implement the methods
fit(X[, y])
transform(X)
Returns
inner (object) : class with decorated methods.
"""
class inner(transformer):
def __init__(self, **kwargs):
"""
Instantiates a transformer object.
"""
# sanity check
required_attrs = ['fit', 'transform', 'fit_transform']
for attr in required_attrs:
if getattr(super(), attr, None) is None:
raise AttributeError("transformer should have {0} attribute".format(attr))
# use underlying estimators machinery
super().__init__( **kwargs)
def fit(self, X, y = None):
"""
1. flattens a 2D array
2. creates rule for transform on the flattened array.
"""
super().fit(X.reshape(-1, 1), y)
return self
def transform(self, X):
"""
1. flattens a 2D array
2. transforms it
3. restores it ot its original shape
"""
X_t = super().transform(X.reshape(-1, 1))
return X_t.reshape(-1, X.shape[1])
def fit_transform(self, X, y = None):
"""
Fits and transforms 2D array via flattening.
"""
x_t = super().fit_transform(X.reshape(-1, 1), y)
return x_t.reshape(-1, X.shape[1])
return inner
Power transform on split data
We should remember ourselves that the temperature and precipitation data have to be scaled separately.
For this end, we write a class which applies transormers to subsets of features. It is akin to FeatureUnion. The main difference is, that a certain transform is applied to a specified selection of the dimensions as opposed to the entire data. This transformer is implemented as the SegmentedFeatureUnion class below. We are going to subclass the aforementioned FeatureUnion class.
from sklearn.pipeline import FeatureUnion, _fit_one_transformer, _transform_one
from sklearn.utils._joblib import delayed, Parallel
class SegmentedFeatureUnion(FeatureUnion):
"""
Applies transformers to selections of features.
Class based on sklearn.pipeline FeatureUnion
"""
def __init__(self, transformer_list, n_jobs = None,
transformer_weights = None, transformer_ranges = None):
"""
Parameters:
transformer_list ([object]) : list of objects that implements the methods
fit : fit(X[, y])
transform : transform(X, [,y])
transformer_ranges ([np.ndarray]) : list of indices to which the transformers are applied.
"""
super().__init__(transformer_list,
n_jobs = n_jobs,
transformer_weights = transformer_weights)
self.transformer_ranges = transformer_ranges
def _iter(self):
"""
Generate (name, trans, weight, transformer_range) tuples excluding None and
'drop' transformers.
"""
get_weight = (self.transformer_weights or {}).get
return ((name, trans, get_weight(name), transformer_range)
for (name, trans), transformer_range in zip(self.transformer_list, self.transformer_ranges)
if trans is not None and trans != 'drop')
def fit(self, X, y = None):
"""
Fit all transformers using X.
Parameters:
X (np.ndarray[n_samples, n_features]) : data to be transformed
y ({np.ndarray[n_samples], None}) : target variable, usually not used
Returns:
self (SegmentedFeatureUnion) : this estimator
"""
self.transformer_list = list(self.transformer_list)
self._validate_transformers()
transformers = Parallel(n_jobs=self.n_jobs)(
delayed(_fit_one_transformer)(trans, X[:, transform_range], y)
for _, trans, _, transform_range in self._iter())
# save fitted transformers --> used in self._iter
self._update_transformer_list(transformers)
return self
def transform(self, X, y = None):
"""
Transform X separately by each transformer, concatenate results.
Parameters
X (np.ndarray[n_samples, n_features]) : data to be transformed
y ({np.ndarray[n_samples], None}) : ignored
Returns
X_t : array-like or sparse matrix, shape (n_samples, sum_n_components)
hstack of results of transformers. sum_n_components is the
sum of n_components (output dimension) over transformers.
"""
x_t = Parallel(n_jobs=self.n_jobs)(
delayed(_transform_one)(trans, X[:, transform_range], None, weight)
for name, trans, weight, transform_range in self._iter())
# stack arrays
X_t = np.hstack(X_t)
return X_t
def fit_transform(self, X, y = None):
"""
Override parents fittransform.
"""
return self.fit(X, y).transform(X, y)
Testing
We can now transform the data according to the following recipe
- split features to temperature and precipitation subspaces
- flatten each subspace
- power transform each flattened array
- mould array to original shape
The power transform will be performed by the FlatPowerTransformer class instances. The underlying class is the PowerTransformer utility of sklearn.
from sklearn.preprocessing import PowerTransformer
FlatPowerTransformer = create_flat_transformer(PowerTransformer)
Separate transformers are then created for the temperature and precipitations subspaces:
transformers = [("trf1", FlatPowerTransformer(method = 'yeo-johnson', standardize = True)),
("trf2", FlatPowerTransformer(method = 'yeo-johnson', standardize = True))]
# 0-->11 temperature; 12-->23 precipitation
transformer_ranges = [np.arange(12), np.arange(12, 24)]
The transformers are then collated in a single SegmentedFeatureUnion instance:
sfu = SegmentedFeatureUnion(transformers, transformer_ranges = transformer_ranges)
A quick test is worth the time on a random array:
X = np.random.rand(100, 24)
# segmented feature union
sfu.fit(X)
X_t = sfu.transform(X)
# setp-by-step
trf1 = PowerTransformer(method = 'yeo-johnson', standardize = True)
trf2 = PowerTransformer(method = 'yeo-johnson', standardize = True)
trf1.fit(X[:,np.arange(12)].reshape(-1, 1))
trf2.fit(X[:,np.arange(12,24)].reshape(-1, 1))
X_t_ref = np.hstack([trf1.transform(X[:,np.arange(12)].reshape(-1, 1)).reshape(-1,12),
trf2.transform(X[:,np.arange(12,24)].reshape(-1, 1)).reshape(-1, 12)])
# compare two transformed arrays
print("-Are the two methods agree within error?")
print("-The computer says: {0}".format(('No-oo...', 'Yes!')[np.allclose(X_t, X_t_ref)]))
-Are the two methods agree within error?
-The computer says: Yes!
Scaling
It is healthy if the input values of the neural network are in the range of $[0,1]$. This can be achieved by appending the sklearn’s very own MinmaxScaler after the Yeo–Johnson transform. Since both the temperature and precipitation data are now scaled roughly to the same range, it is reasonable to apply the MinMaxScaler to the all dimensions of the numeric data without splitting them. The transform should digest the flattened array, thus the we will reuse our create_flat_transformer class factory to create the appropriate transformer.
from sklearn.preprocessing import MinMaxScaler
# create a minmax scaler operating on flattened arrays
FlatMinMaxScaler = create_flat_transformer(MinMaxScaler)
Classification
As promised in the introduction a neural network will be in charge of estalishing a relationship between numerical data and the climate class labels. The network of choice is tensorflow’s keras high level framework. This module contains a wrapper that creates an estimator class compatible with the sklearn API.
KerasClassifier constructor consumes keyword argument. The build_fn keyword requires a function that builds and compiles a network. Additional, user defined keywords can also be passed that are either used to specify the network properties or define particulars of the fit process, such as number of epochs or batch size.
Below a slim manifestation of such a function, model_builder is defined. The sole parameter of this function is the keyword argument layers:
layers: defines the size and activation of the successive layers
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.wrappers.scikit_learn import KerasClassifier
def model_builder(layers = [[10, 'relu'], [10, 'softmax']]):
"""
Mock neural network buider.
Parameters:
layers [[int, str]] : list of lists, where
1. member of tuple : layer size
2. member of tuple : activation type.
Default : [(10, 'relu'), (10, 'softmax')]
Returns
model () : a compiled neural network
"""
# argument checks -- let us assume types are correct
allowed_activations = ('relu', 'softmax')
for idx, (nunit, activation) in enumerate(layers):
if not activation in allowed_activations:
raise ValueError("'activation' must be {0} in position ({1}, 1). Got: {2}" \
.format(" ".join(allowed_activations), idx, activation))
if nunit < 1:
raise ValueError("'nunit' must be greater than zero in position({0}, 1). Got: {1}" \
.format(idx, nunit))
# build model
model = keras.models.Sequential(
[keras.layers.Dense(nunit, activation = activation)
for nunit, activation in layers])
# compile model
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics = ['accuracy'])
return model
So good, so far. We do not the number of labels in advance wich determines the size of the output layer. In fact, it is unknown until the training happens. The problem is the layer keyword argument is passed to the constructor and saved. There is no way updating it when the fit happens in the KerasClassifier class. There is a solution, though. The actual model that performs the classification is not constructed until the fit method is called. By modifying this method in a subclass of KerasClassifier one can set the size of the last layer dynamically.
An issue immediately arises. The parameters of the model_builder cannot be accessed without reflection inside the KerasClassifier class. It is therefore not possible to use set_params to update the layers, unless the keyword layers is explicitily passed to the constructor thereof. Of course, it is legit to always pass this argument, but it is unwiedly and gives rise to making plenty of errors.
Using the inspect module is modestly elegant, but the most straighforward solution. In fact, KerasClassifier realies on it to determine whether a keyword argument is meant to modify the network structure, or it is a directive to the compile or fit methods.
Below, the AdaptiveKerasClassifier class modifies the original fit algorithm, so that the size of the last layer is automatically set by the number of classes in the training sample.
import inspect
class AdaptiveKerasClassifier(KerasClassifier):
def fit(self, x, y, **kwargs):
"""
Trains the neural network on the a given sample.
This method uses KerasClassifier's fit method, but updates the size of the last layer.
"""
n_unit_output_layer = np.unique(y).size
# update the size of the last layer
# 'layers' has been passed explicitly as a parameter
if 'layers' in self.sk_params:
# copy and modify
layers_ = [[n_, a_] for n_, a_ in self.sk_params['layers']]
layers_[-1][0] = n_unit_output_layer
layers_ = tuple(layers_)
# reset sk_params
self.sk_params['layers'] = layers_
# if not in skparams, build_fn uses the default value
else:
# get default with introspection
layers_ = inspect.signature(self.build_fn).parameters['layers'].default
# modify it
layers_[-1][0] = n_unit_output_layer
# add to sk_params
self.sk_params['layers'] = layers_
# invoke parent's fit method
super().fit(x, y, **kwargs)
Assempling the pipeline
Loading data
A simple utility is written to load the raw data and return the numeric observations and labels.
def data_loader(path_to_db):
"""
Loads the climate data.
Parameters:
path_to_db (str) : path to the csv dat file
Returns:
X (np.ndarray[n_samples, n_features], dtype = float) : the observations
labels (np.ndarray[n_samples], dtype = object) : the climate class labels
"""
df = pd.read_csv(path_to_db)
X = df.loc[:,'2' : '25'].values
labels = df['Cls'].values
# free up space
del df
return X, labels
The data are then loaded.
path_to_db = r'path/to/temperature-precipitation-cls.csv'
X, labels = data_loader(path_to_db)
Labels
If the classes are unbalanced it can happen that the training and test sets of labels are not identical. As a consequence, one has take extra care to ensure that they are encoded consistently. To save ourselves from this trouble, the literal labels are encoded for the entire data set before model optimisation.
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
y = encoder.fit_transform(labels)
The Pipeline
We now have all the components of the pipeine to classify the climate data set. These are
- Segmented feature transformation using our
SegmentedFeatureUnionclass - Scaling of the entire data set with the
FlatMinMaxScaler - Neural network classification algorithm wrapped in the
AdaptiveKerasClassifierclass
from sklearn.pipeline import Pipeline
# power transform
power_transformers = [("power_trf1", FlatPowerTransformer(method = 'yeo-johnson', standardize = True)),
("power_trf2", FlatPowerTransformer(method = 'yeo-johnson', standardize = True))]
power_trf = SegmentedFeatureUnion(power_transformers,
transformer_ranges = [np.arange(12),
np.arange(12, 24)])
# scaling
scale_trf = FlatMinMaxScaler()
# classifier
classifier = AdaptiveKerasClassifier(model_builder)
# full pipeline
pipeline1 = Pipeline([('power_trf', power_trf),
('scale_trf', scale_trf),
('classifier', classifier)])
Hyperparameter optimisation
Set of parameters we seek to optimise are
- compositon of preprocessing pipeline
- network architecture
- number of epochs
The optimisation is carried out on a grid where the fitted models are evaluated by a fivefold cross validation.
from sklearn.model_selection import KFold, GridSearchCV
# test various network architectures.
parameter_grid = [{'classifier__epochs' : [5, 7, 10],
'classifier__layers' : [
((128, 'relu'), (10, 'softmax')),
((24, 'relu'), (128, 'relu'), (10, 'softmax'))]
}]
# five fold crossvalidation
cv = KFold(n_splits = 5, shuffle = True)
# using pipeline with minmax scaling
grid1 = GridSearchCV(pipeline1,
param_grid = parameter_grid,
cv = cv,
return_train_score = False)
grid1.fit(X, y)
We now proceed to investigate the effect of the MinMaxScaler by omitting it from the pipeline. This requires updating our pipeline and cross validation object which can be done in two lines. Fortunately, we save an immense amount of work using pipeline and custom esitmators.
# pipeline without minmax scaling
pipeline2 = Pipeline([('power_trf', power_trf),
('classifier', classifier)])
grid2 = GridSearchCV(pipeline2,
param_grid = parameter_grid,
cv = cv,
return_train_score = False)
grid2.fit(X, y)
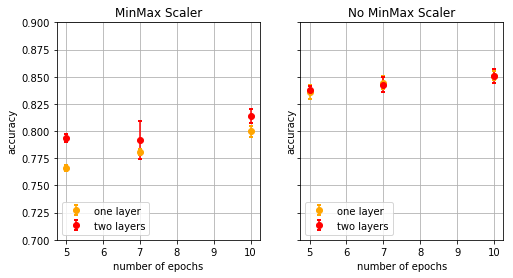
The pipeline with minmax scaling returns results less good (I listened too much PM questions, thus I avoid using the term ‘worse’) than the one from which the scaler is omitted. The reason being bulk of the data is squashed in a region close to zero, which results in low activations in the first relu layer. In other words, we lose information.
The network with two hidden layers outperforms the one with a single middle layer. This is not at all surprising, for it has more flexibility and thus compensate for the information loss.
There is not a significant difference between the two networks where the minmax scaler is not used. One hidden layer has enough variable to parametrise a reasonably good classifier, for the input data are not squashed.
Summary
We have created a data pipeline that transforms and classifies the climate data set. Most of the work consisted of writing wrappers around existing sklearn and tensorflow utilities.
Neural network classifiers have also been trained and their performance examined. It has been established the range of the input data has a significant impact on the accuracy of the the classifiers.