Flags 5.: Topology

02 Oct 2020

Introduction

The topological features of the flags are investigated in this post. We will use it to uncover the various families of canvas designs.

Data

Raster images

We will use high resolution png images throughout this log post. They were obtained from pdf images as detailed in the previous post.

Image preprocessing

The coat of arms have been replaced by a uniformly coloured area in each flag to reduce complexity. Some flags were further modified:

Coding

As usual, only the relevant snippets of code are shared in this blog post. The raw notebook can be found here. The longer scripts are stored in this folder.

Preliminaries

Country codes

Each country is identfied through its two letter code.

with open(os.path.join(folder_lookup, "iso-country.json")) as fp:
    ccodes = json.load(fp)

Loading images

The images are loaded through a generator to avoid keeping large amount of data in the memory.

def create_image_loader(folder, func, tokens, ext):
    """Creates a generator of generator of images."""
    while True:
        gen_path = ((x, os.path.join(folder, f"{x}.{ext}")) for x in tokens)
        generator = ((k, func(v)) for k, v in gen_path)
        yield generator

An image loader is created straight away:

loader = create_image_loader(folder_simplified, imread, ccodes.keys(), "png")

Encoding

We are only interested in whether two colours are indentical or not irrespective the actual value of the colours themselves. The RGB colours are thus mapped to a field of one byte label for each flag.

def label_encode_image(image):
    """Returns an array of colour indices."""

    records = np.ascontiguousarray(image)\
              .view(np.dtype((np.void,
              image.dtype.itemsize * image.shape[-1])))

    labels, idcs = np.unique(records, return_inverse=True)
    image_new = idcs.reshape(image.shape[:2]).astype(np.uint8)
    
    return image_new

Results

A number of graphs will be created for each country. These will be stored in a central object, the connectivity dictionary.

connectivity = {}

Inner connectivity

Segments and connection

Each continuous region of the same colour is a segment. Each flag can be decomposed to a collection of segments. Two segments are connected is there is a section of finite length along which they touch each other. The way they are connected to each other defines the topology of a flag.

Implementation

Connected component labeling – image segmentation

An image is segmented in a one-sweep breadth first search. The algorithm array-segmenter iterates over the pixels of an image. The colours in a pixel’s four-neighbourhood are compared to the central colour. If any matches its label is set to that of the central pixel and it is added to the queue.

The array_segmenter algorithm returns an image where each segment has a unique label. It performs am exhaustive breadth first search over the pixels.

@nb.jit(nopython=True)
def array_segmenter(image):
    """Labels the connected components in a 2D image"""

    # 
    im = image + 0
    nh, nw = im.shape[:2]
    
    not_found = False
    segment_counter = 0
    next_starts = [[nh//4, nw//4]]
    
    while np.any(im > -1):
        
        # get new i, j
        ii, jj = np.nonzero(im > -1)
        
        if len(ii) == 0:
            break
        else:
            i, j = ii[0], jj[0]
            queue = [[i, j]]
            active = im[i, j]
            
        segment_counter -= 1
        im[i, j] = segment_counter
        
        while len(queue) != 0:
            
            i, j = queue.pop()
            
            nbs = [(i-1, j), (i+1, j), (i, j-1), (i, j+1)]

            for k, l in nbs:
                if (-1 < k  < nh) and (-1 < l < nw):
                    if im[k, l] == active:
                        im[k, l] = segment_counter
                        queue.append([k, l])

    # flip sign
    im *= -1
    
    # shift to zero
    im -= 1

    return im

Determining connectivity between segments

The horizontal and vertical borders are determined. The labels are read from each side of the borders from which pairs are created. The components of these pairs are order to avoid creating duplicates. Finally, a set of pairs is formed which containes the connectivity information between segments. The result is a connecivity graph of the segments.

def get_segment_connectivity(image):
    """
    Determines the connectivity between image segments.
    """
    
    # horizontal borders
    i, j = np.nonzero(np.diff(image, axis=1))
    connectivity = set(zip(image[i, j], image[i, j+1]))
    
    # vertical borders
    i, j = np.nonzero(np.diff(image, axis=0))
    connectivity |= set(zip(image[i, j], image[i + 1, j]))
    
    # remove duplicates
    connectivity = set((min(x), max(x)) for x in connectivity)
    
    return connectivity

Processing

The images are loaded, encoded, segmented and the connectivity thereof is determined.

encoded = ((k, label_encode_image(v)) for k, v in next(loader))
segmented = ((k, array_segmenter(v)) for k, v in encoded)

connectivity["segments"] = {
    k: get_segment_connectivity(v)
    for k, v in segmented
}

Analysis

The raw output looks as follows:

sel = ["FR", "LU", "BF",  "PL", "CH"]

for k in sel:
    print(f"Connectivity of {ccodes[k]}: {connectivity['segments'][k]}")

Connectivity of FRANCE: {(0, 1), (1, 2)}
Connectivity of LUXEMBOURG: {(0, 1), (1, 2)}
Connectivity of BURKINA FASO: {(0, 1), (0, 2), (1, 2)}
Connectivity of POLAND: {(0, 1)}
Connectivity of SWITZERLAND: {(0, 1)}

The flags of France and Luxembourg and Burkina Faso have three segments: 0, 1, 2. One connects to two and two connects to one. The Swiss flag is composed of two regions 0, 1 which are connected to each other. Just like the polish flag. As we can see, the topology is insensitive to the orientation of the flag.

png

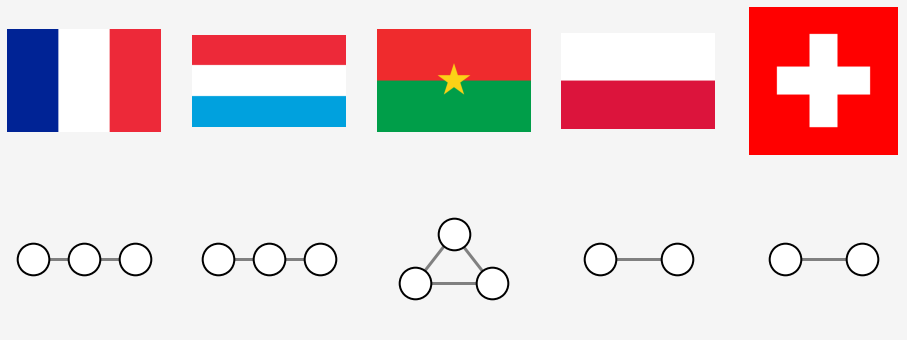
Border region

The Polish and Swiss flags have the same topological representation. However, one might argue that they are different in a topological sense for the white area is enclosed by the red one in the latter one. This ambiguity can be resolved by adding a border region which skirts an entire flag. Only one area, the outer one, would be connected to this new region, whilst the inner one remains only attached to the outer one.

Implementation

The get_border_connectivity function screens along the one pixel wide edges of a flag and creates links to the border region will have the label -1.

def get_border_connectivity(image, single_region=True):
    """
    Determines the connectivity to the border region of a flag.
    """
    
    vals = (
        [-1, -3, -5, -7],
        [-1, -1, -1, -1]
    )[single_region]
    
    slices = ((0, ...), (-1,...), (..., 0), (..., -1))
    borders = (_get_padded_array_set(image[x], v) for x, v in zip(slices, vals))
    connectivity = reduce(set().union, borders)
    
    return connectivity


def _get_padded_array_set(x, val):
    """
    Creates a set of label tuples.
    """
    return set((val, x) for x in np.unique(x))

The inner and border connectivities are calculated in one sweep and then merged:

encoded = ((k, label_encode_image(v)) for k, v in next(loader))

# segment images
segmented = ((k, array_segmenter(v)) for k, v in encoded)

# calculate the two type of connectivities
connectivity["single-border"] = {
    k: (
        get_segment_connectivity(v),  # inside image
        get_border_connectivity(v)    # connectivity with the border
    )
    for k, v in segmented
}

# merge the two connectivities
connectivity["single-border"] = {
    k: v[0].union(v[1])
    for k, v in connectivity["single-border"].items()
}

Analysis

The same flags along with their representations are replotted. Two singly linked nodes appear now under the Swiss flag which clearly distinguishes it from the graph plot of Poland. The latter one forms a triangle.

png

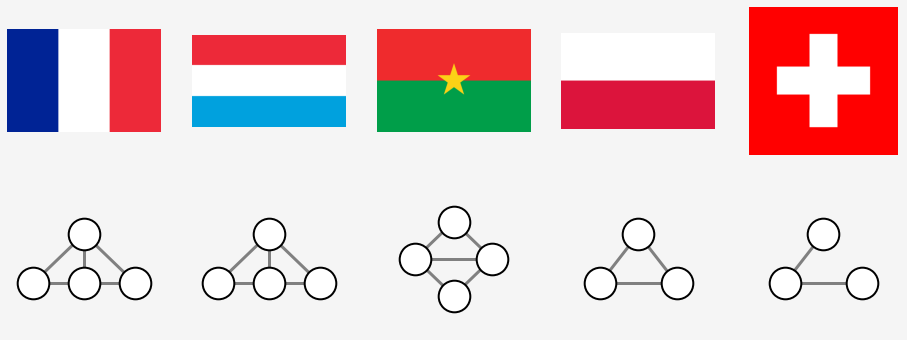
The following can be deduced

The second point leads to ambiguity again. The topological plots of France, Luxembourg and Burkina Faso are identical, despite their topology being different. There are two ways to resolve this issue

The first approach implicitly includes the second one, for the node index of the outer region needs to be known in advance in order to draw the edges. We therefore proceed to colour the nodes in the following.

png

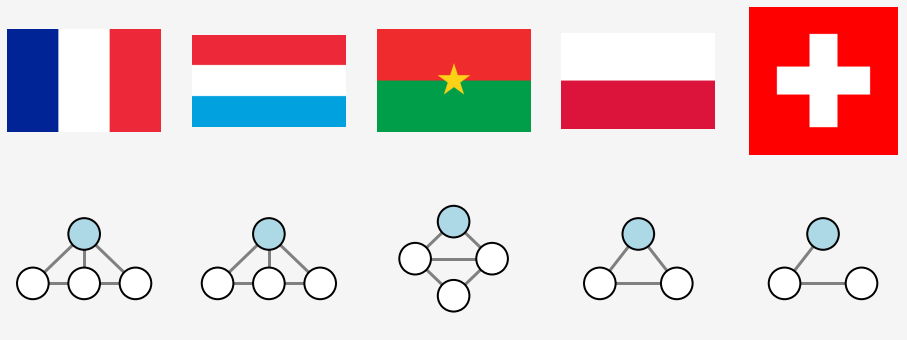
The coloured graphs are now different for each flag as expected.

Isomorphism

A graph is isomorphic to an other if it is possible to relabel its nodes to create a one-to-one mapping between its nodes and edges and those of the second graph. As such, it is an excellent tool to groups topologically identical flags.

Isomorphism rule

Two nodes are considered identical if they are both segment nodes or border nodes.

Implementation

We are going to invoke the GraphMatcher function of the networkx package. Firstly, we need a function that adds a flag to each node indicating whether it is a segment node or not.

def label_nodes_single(g):
    """
    In place labeling of nodes.
    + 1: segment node
    - 1: border node
    """
    attr = {k: {"sg": copysign(1, k)} for k in g.nodes}
    nx.set_node_attributes(g, attr)

Secondly, a function is created which decides whether two nodes are of the same type.

def match_node_type_single(attr1, attr2):
    """
    Decides whether two nodes are of the same type.
    """
    res = 0 < (attr1["sg"] * attr2["sg"])
    return res

The labeled graphs are then created.

graphs = [(k, nx.from_edgelist(v)) for k, v in connectivity["single-border"].items()]
gen = (label_nodes_single(v) for k, v in graphs)
_ = reduce(lambda x, y: None, gen)

It is rather expensive to compute the graph isomorphish. Henceforth a number of shortcuts are introduced:

classes = defaultdict(set)
for i, (k1, g1) in enumerate(graphs):

    # isomorphism is transitive
    if any(k1 in v for v in classes.values()):
        continue
        
    for k2, g2 in graphs[i:]:
        
        # if it has not been found, it is in its own class
        if k1 == k2:
            classes[k1].add(k1)
            continue
        
        # not equal number of nodes, skip comparison
        if len(g1) != len(g2):
            continue
            
        # compute isomorphism
        matcher = GraphMatcher(g1, g2, node_match=match_node_type_single)
        
        # add to classes
        if matcher.is_isomorphic():
            classes[k1].add(k2)

Analysis

There are, in total, 78 classes. It turns out that quite a few countries display starts in their flags the number of which varies greatly. This is the main contributing factor to this large number of classes.

The non-singleton classes with their cardinalities are plotted below.

png

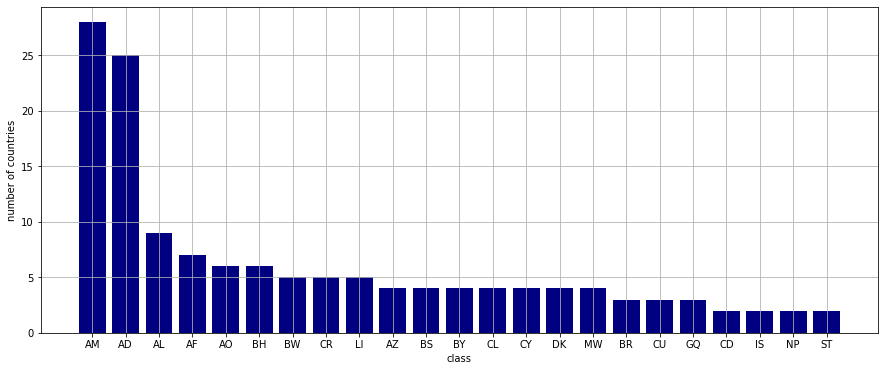
Each class is identified by the label of the country whose country code happens to come first alphabetically. For example,

In general, the more nodes and edges a flag has the fewer of its like can be found.

png

Inheritance

One can quickly recognise the some flags can be derived from other via simple manipulations

For instance,

or

By the repeated application of splits and merges all flags can be created from a few simple ones. These operations correspond to adding (or removing) nodes and edges. In graph parlance, if a subgraph of a graph is isomrophic to a full graph, it can be derived from the smaller graph. Therefore finding subgraph isomorphisms is equivalent to determining the family tree of flags in oru case.

Implementation

A graph from each class is retreived:

class_graphs = [x for x in graphs if x[0] in classes.keys()]

A directed graph is built. Each node of it is a flag graph. An edge point from a parent to its child. If $\mathcal{G}$ is a subgraph of $H$ then $G$ is a parent of $H$ and an edge $(G, H)$ is added to the family graph.

The edges are located by the GraphMatcher:

edges = []
for i, (k1, g1) in enumerate(class_graphs):
    for k2, g2 in class_graphs[i+1:]:
        
        if len(g1) > len(g2):
            
            matcher = GraphMatcher(g1, g2, node_match=match_node_type_single)
            is_subgraph = matcher.subgraph_is_isomorphic()
            
            if is_subgraph:
                edges.append((k2, k1))

        elif len(g1) < len(g2):
            
            matcher = GraphMatcher(g2, g1, node_match=match_node_type_single)
            is_subgraph = matcher.subgraph_is_isomorphic()
            
            if is_subgraph:
                edges.append((k1, k2))
            
        # isomorphism -- already handled
        else:
            continue

The family tree is created from the edges.

family_tree = nx.DiGraph()
family_tree.add_edges_from(edges)

The resultant tree, however, contains not only the immediate parent–child, but the greatparent–child and higher level connections. These are removed to have a clean tree. get_clean_levels works is two steps. Firstly, all offsprings of each generation are found starting from the head. The second step removes those descendants who are not immediately linked to any of their ancestors.

def get_clean_levels(g):
    # find top level
    heads =[x[0] for x in g.in_degree() if x[1] == 0]
    
    # find all children
    parents = set(heads)
    successors = []
    for i in range(len(g)):
        children = set(chain(*(g.successors(p) for p in parents)))
        if len(children) == 0:
            break
        successors.append(children)
        parents = children
        
    # remove non-immediate children
    clean = [set(heads)]
    for i, level in enumerate(successors):
        clean.append(level - set(chain(*successors[i+1:])))
        
    return clean

The create_clean_graph utility constructs a graph from these one egde long connections.

def create_clean_graph(g, levels):
    h = nx.DiGraph()
    for l1, l2 in zip(levels[:-1], levels[1:]):
        edges = (e for e in product(l1, l2) if e in g.edges)
        h.add_edges_from(edges)
        
    return h

The two functions applied in sequence yield a clean family tree.

levels = get_clean_levels(family_tree)
family_tree_clean = create_clean_graph(family_tree, levels)

The family tree of all classes are displayed below. There are two head nodes Bahrain and Albania. Both have two nodes (or regions). They cannot be derived from each other by adding nodes. All of the flags can be constructed from these two by splitting regions or adding new ones.

png

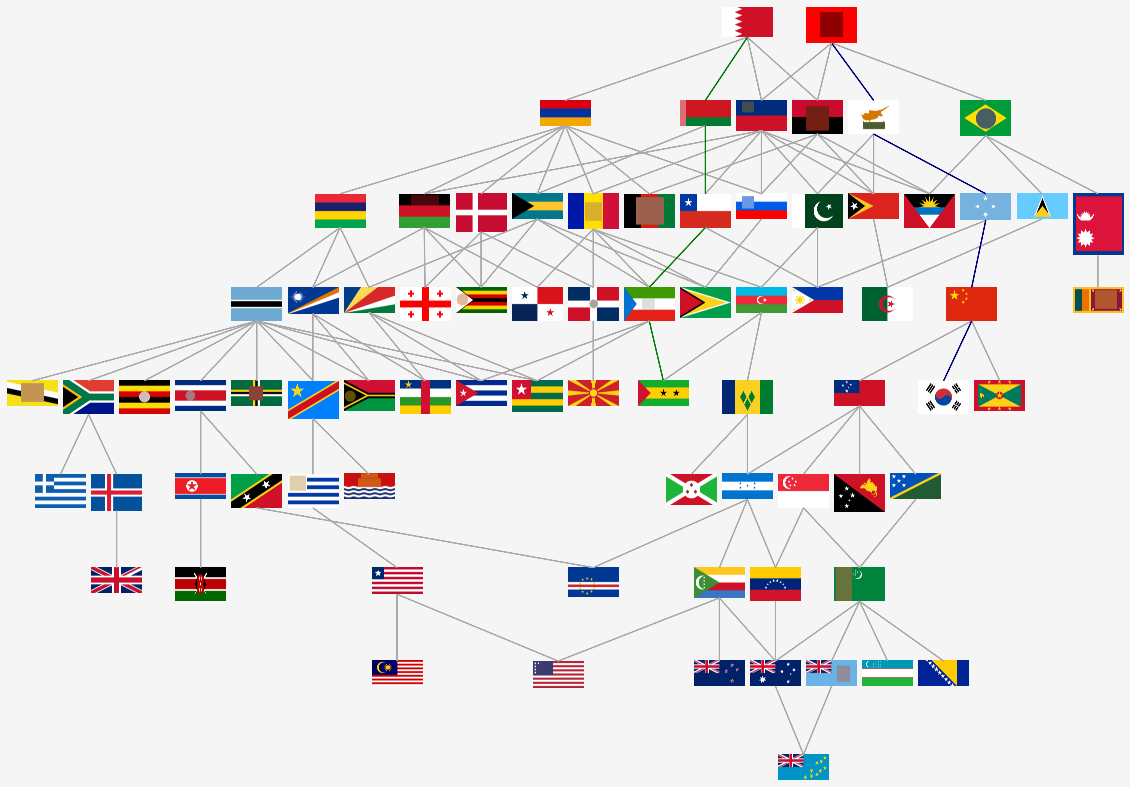
Two paths are examined in detail.

Bahrain to Sao Tome and Principe (green trail)

Albania to Samoa (blue trail)

png